光线追踪
- 作者:admin
- /
- 时间:2022年02月07日
- /
- 浏览:5727 次
- /
- 分类:厚积薄发
本文首先将会介绍光线追踪的类别族谱,介绍其公共部分,之后我们会分别对其中的每一个进行详细地剖析。
光线追踪(Ray tracing)是一个拥有历史感的词汇。图形学从业者从neutron transport、heat transfer和illumination engineering等领域引进其思想。由于这些概念被许多领域所研究,导致光线追踪的术语在学科之间和学科内部都进行着不断发展,有时也会产生分歧。经典的论文也可能会错误地使用术语,这就可能会造成混淆。所以,在介绍光线追踪的概念之前,我们需要分清楚这些术语的概念。
几乎所有的现代光线追踪器都是使用递归和蒙特卡罗方法;但是现在已经很少会有人把他们称为“递归的蒙特卡洛”方法。
一.光线追踪族谱
1.Ray Casting。1968年,Arthur Appel。
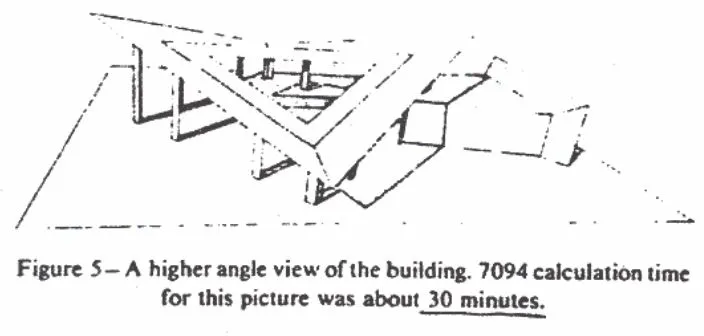
2.Whitted 光线追踪。1980年,Whitted,Kay和Greenberg提出了使用递归的光线追踪来描绘准确的折射和反射。

3.分布式光线追踪。1984年,Cook等人提出了分布式光线追踪(distributed or distribution ray tracing,DRT)。但是,这种方法通常被称为随机光线追踪(stochastic ray tracing),来避免与分布式处理(distributed processing)混淆。其和path tracing都使用了蒙特卡洛方法。

4.路径追踪。1986年引入了两个重要的算法。Kajiya将积分输运方程(integral transport equation)称为渲染方程(rendering equation)。他提出的渲染方程成了至今为止几乎所有的全局光照算法的数学依据,在同篇论文中他也提出了最原始路径追踪算法。

5.双向路径追踪(BidirectionalPath Tracing)由Lafortune和Willems提出,Veach则对双向路径追踪做了详细的描述。

6.Metropolis Light Transport。1997年Veach首次将最早应用在计算物理领域的Metropolis采样方法引入图形学。

7.Energy Redistribution Path Tracing 2005

8.Manifold Exploration 2012

二.Ray Casting
第一个用于渲染的光线投射算法最初由Arthur Appel在1968年引入。光线投射通过从观察点对每一个像素发射一条光线并找到在世界场景中阻挡光线路径的最近物体来渲染场景,Ray Casting只有两种射线,第一种是眼睛发射的eye射线,来寻找场景中的交点,另一个是从交点发到灯光的阴影射线,看自身是否是处于阴影当中。与传统扫描线渲染算法相比,光线投射的一个显着优点是能够处理不平整的表面和固体。电子世界争霸战(1982年电影Tron Series)的大部分动画都是使用光线投射技术渲染的。
早年间光栅化技术还未流行时,也会用于游戏当中。最著名的一款光线投射的游戏是Wolfenstein 3D。接下来将介绍不论在光线追踪还是光线投射算法中都通用的公共部分,避免之后的内容太过的庞杂。
2.1 光线投射基本算法
Render()
for each pixel x,y
color(pixel) = Trace(ray_through_pixel(x,y))
首先做的就是创建光线,得到每一个点的光线数据结构,之后开始Trace,这里使用Trace这个函数名是为了和后面统一。是指在场景中追踪这个光线。
Trace(ray)
object_point = Closest_intersection(ray)
if object_point return Shade(object_point, ray)
else return Background_ColorRender()
for each pixel x,y
color(pixel) = Trace(ray_through_pixel(x,y))
我们在场景中寻找光线与场景中的物体是否有交点,并返回距离我们最近的那一个object的信息,如果找到,我们进行着色如果没找到我们返回设定的背景颜色。
Closest_intersection(ray)
for each surface in scene
calc_intersection(ray, surface)
return the closest point of intersection to viewer
在光线投射的Closest_intersection中,我们并不需要额外的返回其他的复杂信息。
Shade(point, ray)
to calculate contributions of each light source
光线投射的着色,你可以自由发挥,最初的实现中也只有阴影的划分。对于像Wolfenstein 3D这样的实时游戏中的场景,一般是使用了额外的场景信息,来提高性能。总之这里的shade并不重要,主要是理解RayCast这个思想框架,而之后的所有算法都是在这个框架中的发挥。
当然我们也可以进行简单的着色计算,这就和不进行递归的RayTracing是一致的,我们放在之后来做对比。
2.2 光线的表示和求交问题
不论对于哪种的光线渲染算法,第一步都是进行从相机进行光线投射,其最终的目的就是找到屏幕中的每一个像素对应的光线的方向。
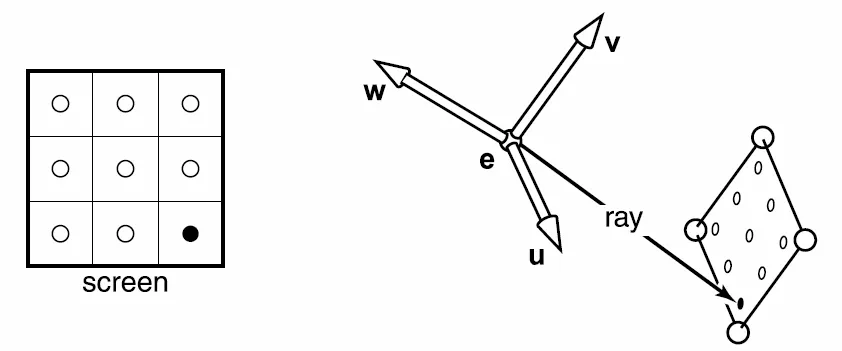
在这里,对于局部、世界和相机空间的转换关系是和光栅化渲染中的空间转换的做法基本类似,所以在这里就不进行赘述。
大多数情况下,我们使用 p(t)=e+t(s-e) 的方法来进行光线的表示,e是我们设定的相机观察点,而s是画布上的点,通常我们渲染之前预先设定的长宽,然后我们通过参数t来表示光线的长度。
- 当t为0,表示原点
- 当t为正数代表正向我们的方向
- 当t为负数代表在原点后面
- 如果t1<t2,代表t1离我们更近
对于求交问题,网上非常多的资料,这里就不讲了,只给出思路和参考资料。
这里有一个对于物体来说是显示表示还是隐式表示法的问题。
三.Whitted RayTrace
光线投射渲染的进化发生在1979年,当时Turner Whitted通过引入反射,折射和阴影来延长光线投射过程从而形成自身的Whitted光线追踪。

在当时它得到的那张512x512的渲染图耗时74分钟,而今天则只需要几秒钟就可以完成。
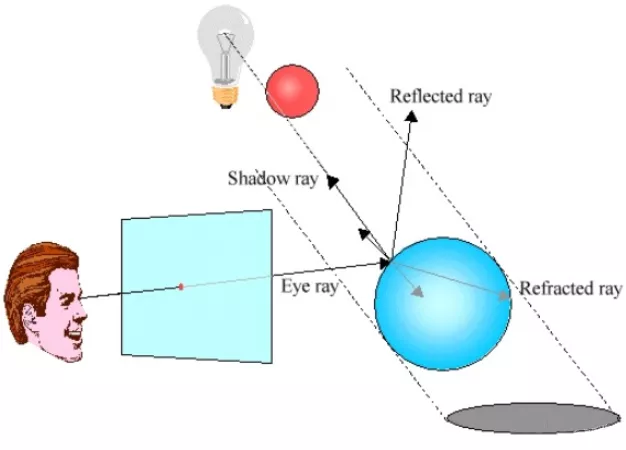
大致上,Whitted RayTrace其主要把光线分为四种:
- 视角光线,和之前的一样,没什么好说的。
- 反射光线。在表面沿镜面反射方向继续照射。反射的颜色由反射光线与场景中的对象的交点决定。
- 折射光线,其创建与反射光线类似,只是它的方向是进入对象并最终可以退出对象。
- 阴影光线,是通过创建从交点到所有灯光的阴影光线来计算的。如果阴影光线在到达灯光之前与某个对象相交,则该交点将从该特定灯光中阴影显示。
Whitted光线追踪主要解决了场景中没有间接光的问题,但是它解决的也相当的一般,因为它所有的间接光都只来源于完美的镜面反射或者是折射,这种材质显然在现实世界中并不常见,对于大多数的间接光基本无法模拟,这也是由于它对每一个EyeRay的交点只发出一条的Reflected ray和Refracted ray。这个问题将在分布式光线追踪中有所改善。
3.1 光线追踪的类型
3.3.1 前向光线追踪 Forward Ray Tracing
前向光线追踪遵循光子从光源到物体。虽然前向光线可以最准确地确定每个物体的颜色,但效率非常低。这是因为来自光源的许多光线永远不会通过视平面并进入眼睛。追踪来自光源的每条光线意味着许多光线将被浪费掉,因为它们从未对从眼睛看。(这里的前向后向可能每个人理解不同而相反,这里指的是Light Ray Tracing。)
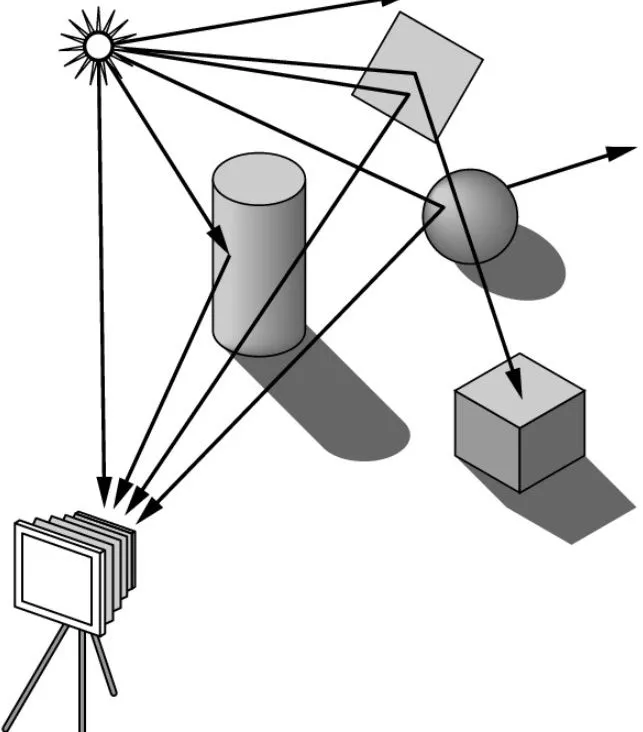
3.1.2 向后光线追踪 Backward Ray Tracing

为了使光线追踪更有效,引入了后向光线追踪方法。在后向光线中,在眼睛处产生眼睛光线;它通过视平面并进入世界。射线击中的第一个物体是从视平面的那个点可见的物体。
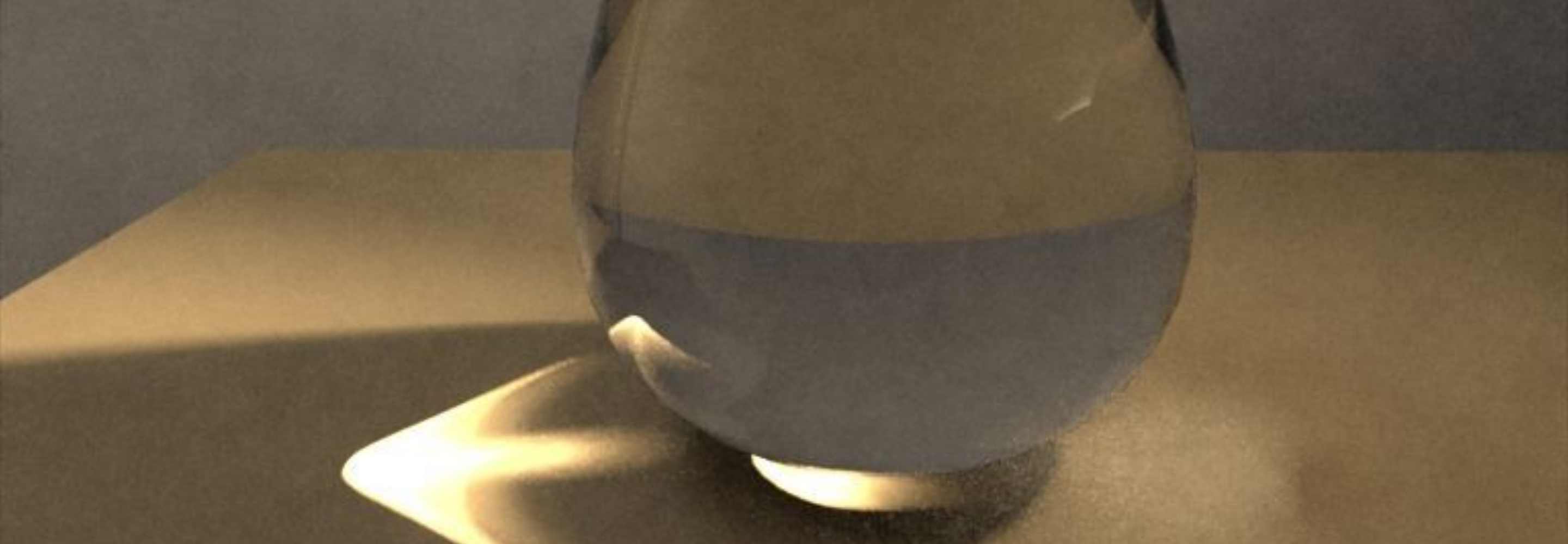
后向光线的缺点是它假设只有通过视平面并进入眼睛的光线对场景的最终图像有贡献。在某些情况下,这种假设是有缺陷的。例如,如果一个透镜被固定在桌子顶部的一个距离处,并且被正上方的光源照亮,那么在透镜下面会有一个具有大光浓度的焦点。如果反向光线追踪试图重新创建此图像,则会计算错误,因为向后发射光线只会确认光线通过透镜;反向光线无法识别通过透镜的正向光线弯曲。因此,如果只进行反向光线追踪,透镜下方将只有一个均匀的光斑,就像透镜是一块普通的玻璃。
如上所述,有效且最容易实现性能优化的一种方法是从眼睛向后发射光线,而不是从光源光发射线。通过这种方式,不会浪费计算能力来从未击中模型或相机的光线。
3.1.3 混合光线追踪
由于前向光线追踪和后向光线追踪都有其缺点,最近的研究试图开发出会影响速度和精度的混合解决方案。在这些混合解决方案中,仅执行某些级别的前向射线。算法记录数据,然后继续执行后向光线追踪。场景的最终着色将后向光线和前向光线计算都考虑在内。
Veach(1995)发明出了后向光线追踪+前向光线追踪+连接线(Bidirectional Path Tracing)的混合方法,这在后面会讲解。
综上,而我们的Whitted光线追踪一般而言都时使用的向后渲染的方式来进行的(从眼睛发射光线)。
3.2 光线追踪基本算法
我们在第二部分聊的Shade部分,在这里就有了用途。我们知道递归是光线追踪的最基本的特点,我们先来看没有递归的情况。其实没有递归的情况和RayCasting技术特点几乎是一模一样的。
之前的框架是一样的,所以这里就不都列出来了,只列出不一样的部分。
Shade(point, ray)
calculate surface normal vector
use Phong illumination formula
to calculate contributions of each light source
首先如之前所列的年代关系,出现Whitted光线追踪时,并没有提出我们现在做全局光照的渲染方程,所以当时依旧是使用的基于经验的光照模型,就像这里的phong。当然你也可以用其他的。
我们来看递归的形式:
Shade(point, ray)
radiance = black; /*初始化 */
for each light source
shadow_ray = calc_shadow_ray(point,light)
if !in_shadow(shadow_ray,light)
radiance += phong_illumination(point,ray,light)
if material is specularly reflective
radiance += spec_reflectance * Trace(reflected_ray(point,ray)))
if material is specularly transmissive
radiance += spec_transmittance * Trace(refracted_ray(point,ray)))
return radiance
首先进行这个点的颜色初始化,如果不在阴影中,我们phong模型的着色,如果材质拥有镜面反射,最后的颜色要加上镜面反射光线的颜色贡献,如果材质拥有折射特性,加上折射的贡献。
当然,这里对于放射和折射的具体计算比较基础,就不表了。搞了这么多,我们先不进行其他的分析,先来看看效果上和RayCasting的区别:

递归两次

递归三次
还有一个比较重要的问题是什么时候结束这个罪恶的递归?有两种情况。第一种情况是,光线没有打到物体上,第二种是由于每一次反射或者折射,贡献值会逐渐的降低,我们预先设定一个阈值,当它小于这个阈值的时候,我们停止。当然,如果你只按照上面的做法来渲染一个图片出来是可行的,但是会有一些需要解决的问题。
3.3 锯齿

我们首要问的问题时,为什么会产生锯齿?由于之前的光线追踪算法对每一个像素值,都只创建了一个光线,都只采样了场景中的一个点,和那一个颜色,但是,对于一个像素而言,有可能包含了很多个不同的点,尤其是在物体边缘的情况下时,这些点不一定都有相同的颜色。而我们这种有规律的采样,就会导致这种锯齿。
3.3.1 超级采样
超级采样是为每个像素增加的光线数量的过程。这不能解决锯齿问题,但它会尝试减少它们对最终图像的影响。在以下示例中,从像素发出九条光线。六个是蓝色,三个是绿色。像素的最终颜色将是蓝色的三分之二和绿色的三分之一。

当然也可以有其他的组合方式,数量位置和比例上都可以自行设定。

3.3.2 自适应超级采样
自适应超级采样(也称为蒙特卡罗采样)是一种以更智能的方式进行超采样的尝试。首先发出固定数量的光线并比较它们的颜色。如果颜色相似,则程序假定像素正在查看同一个对象,并且光线的平均值被计算为该像素的颜色。如果光线颜色不同(由某个阈值定义)那么我们认为这个像素比较特殊需要进一步检查。在这种情况下,像素被细分为更小的区域,并且每个新区域被视为一个完整的像素。这个过程再次开始,同样的固定光线模式被射入每个新的部分。
遗憾的是,自适应超级采样仍然将像素划分为规则的光线模式,并且会受到常规像素细分可能出现的混叠的影响。例如对象和采样网格几乎是对齐的。总之有规律的方法都不得劲。
3.3.3 随机采样
Stochastic(随机)采样将固定数量的光线发送到像素中,但确保它们是随机分布的(但或多或少均匀地覆盖该区域)。此外,Stochastic射线试图解决在凹凸不平的表面上跟随入射光线的问题。这是分布式光线追踪中比较核心的概念,所以放在下面来说。
3.4 加速结构
加速结构用于限制要检查的对象数量以找到与谁相交的技术。例如,如果我们有一条射线,它将一个物体与数千个物体相交,我们想以某种方式智能地清除远离光线的物体。
3.4.1 包围盒(Bounding Volumes)
基于层次关系的划分方法中包围盒层次结构最有代表性。层次包围盒算法的基本思想是:用形状简单的包围盒(如球形、长方体等)将场景中的面片包围,相邻的包围盒被包含在一个更大的包围盒里,逐级扩大,生成一个层次的结构;在进行光线与物体相交测试之前,先进行光线与包围盒的测试,如果光线与包围盒相交,再与其包含的物体面片进行相交测试,提高效率;通过将包围盒按照有效的层次结构进行组织,减少进行相交测试的数目,降低复杂度,进一步得到效率上的提升。在包围盒的选取中,一方面应该选择形状简单的包围盒,降低光线与包围盒相交测试的代价;另一方面应该选取能够紧密包围物体面片的包围盒,提高光线与包围盒进行相交测试的有效性。
在实际应用中,最常用的是轴对称包围盒(Axis Aligned Bounding Box,AABB)。AABB轴对称包围盒简便,易于存储,易于计算,鲁棒性好,是对相交测试简便性和包围物体紧凑性的较好折中,效率较高。与基于空间分割的划分方法相比,基于层次关系的划分方法在动态场景中更有优势。因为,在动态场景中,场景的组织结构都要变化,每一帧都要重新构建,这无疑是巨大的开销,导致计算量激增。在动态场景中,基于层次关系的划分方法形成的数据结构,可以只更新相关包围盒的有关信息(如其位置和大小)。也就是说,BVH只需要进行数据结构的刷新,而不需要进行重建,这样在效率上有明显的提高。
- 快速拒绝:首先根据包围体检查光线
- 更快的拒绝:检查视锥体对象的包围体
一种组织结构是在将包围体分组到包含的包围体中,以创建自下而上的树层次结构,在命中包围体时,递归检查其子节点。

3.4.2 均匀网格
空间网格是把三维空间分别沿着三个方向轴以特定宽度划分,得到一定分辨率的网格,场景中的面片都被分配到相应的网格中。每个网格可以含有不同的面片,每个网格保存其所包含的场景面片的引用。最简单的便是均匀网格,把场景进行均匀划分。
生成均匀网格并创建一个结构,将每个网格位置与网格位置中的另一个对象链接起来。对于光线接触的每个网格,检查对象是否与光线相交。
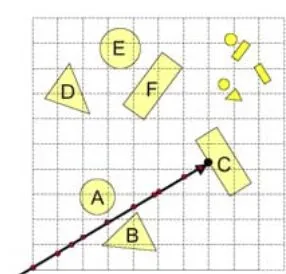
这种方法的优点便是方便简洁,易于创建,并且可以快速将场景中的面片分配到相应的网格中。然而,在实际的场景中,面片的分布是比较不均匀的,比如大多数的面片集中在少数几个网格中,则当进行光线遍历时需要遍历很多面片,也有可能一次相交测试能够踢除的无关面片非常少,遍历过程很麻烦。所以,如果场景中面片分布不够均匀的时候,这种分割方法的遍历效率非常低。
3.4.3 KD-Tree
BSP树是一种空间分割技术,在许多领域都有所应用,于20世纪90年代被引入到计算机图形学的各个研究领域和应用场合。KDTree可以看作是BSP树的一种特例,它是推广到多维空间下的树形结构。原理是将整个场景作为一个树,通过分割平面将当前树划分为两个空间得到两个子树,这两个子树又分别被各自的分割平面分割得到更小的子树,直到树的深度达到预定的阈值或者节点中含有的场景面片数小于预定的阈值。树的每个节点表示一个子空间,囊括所代表空间中包含的所有面片,树的根节点代表整个景空间。
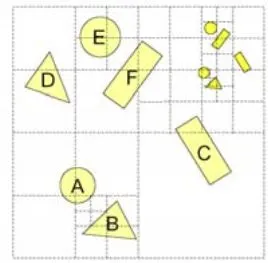
以后单独讲这一块,下面的东西还非常的多,主线上不能丢下。
四.分布式光线追踪(distributed ray tracing,DRT)
我们终于即将触摸到现代的使用蒙特卡洛方法的光线追踪方法-分布式光线追踪。分布式光线追踪不是分布式系统上的光线追踪。分布式光线追踪是一种基于随机分布采样的光线追踪方法,用于减少渲染图像中的瑕疵。起初我们叫distributed ray tracing,后来叫它distribution ray tracing,为了区分parallel computing。我们根据特点也称其为stochastic ray tracing。为什么叫这个名字呢,看下去就知道了。那我们就有一个重要的问题出现了:我们为什么不满足Whitted光线追踪的效果,要不断地发明创造呢?

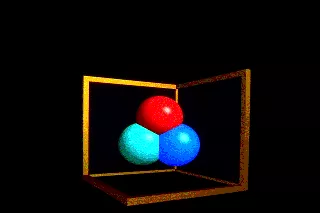
观察上图,随便一个普通人都可以非常清楚地断定,这是一张计算机渲染出来的图像而不是相机照下来的图片。因为它拥有完美的反射,表面也是完美的颜色,并且有生硬的影子,难看的锯齿,没有景深。我们称这种现象为失真。甚至在Kajiya(1986)形式化渲染方程之前,Cook等人就认识到渲染只是解决一组嵌套积分的过程。这些积分没有可以在有限时间内计算的解析解,所以使用蒙特卡洛解决这些问题的技巧。在Cook的distributed ray tracing(1984)解决了这些问题,我们可以进行总结其特点:
- 使用非均匀(抖动,jittered)采样
- 使用噪点noise代替图像失真的情况
- 提供了一些特效,如Glossy reflections、Soft shadow、Motion Blur、Time等
分布式光线追踪的主要思想是,之前我们对每一个像素进行超采样可以进行求平均值的方式来进行抗锯齿的操作,那么也可以不光只在一开始eye Ray发出多个射线,也可以在每次反射折射时也发出多条射线,这能做到比whitted光线追踪的单条反射折射射线更多的事情和效果。
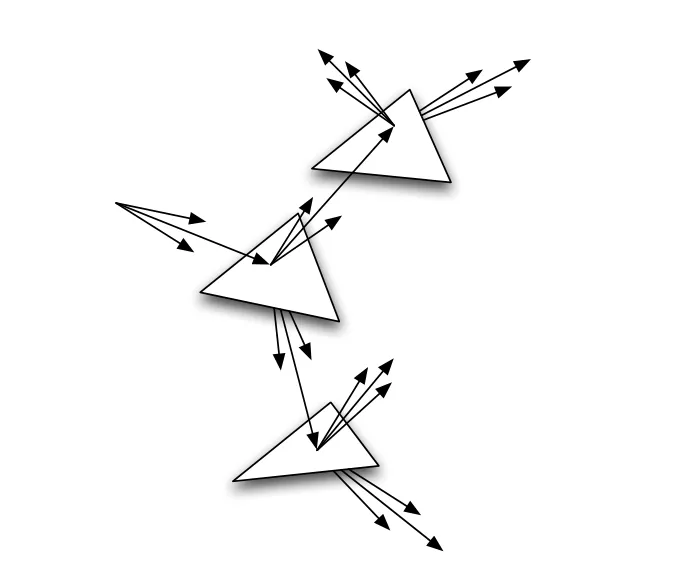
最值得我们关注的问题其实是,在1986年当渲染方程被归纳出来之前,1984年的Cook的论文缺乏真正推理它的数学框架,分布式光线追踪缺乏对全局照明效果的任何描述。所以你确实可以随意地发挥确保他符合LIT。
基本的直接光间接光的采样方式和path trace一样,在下一节介绍。
4.1 针对像素的采样
正如之前我们在Whitted中讲到的抗锯齿的方法一样,如果没有随机性的话,不管怎样都会出现特殊的情况从而导致错误。所以,我们分布式光线追踪中使用的就是随机采样的方式(stochastic sampling),这种方法避免了像网格抽样的那种规律性。
4.1.1 泊松圆盘采样(Poisson Disk Distribution)
一个采样位置不均匀分布的例子就是眼睛,眼睛有有限数量的光感受器,就像其它采样过程一样,应该是有一个奈奎斯特极限(Nyquist limit),但是眼睛正常情况下是不会发生锯齿现象的。在眼睛的中央窝(Fovea)中,六边形图案的细胞是紧密排列起来的,晶状体就扮演着低通滤波器的作用,这就避免了锯齿的发生。但是在中央窝外部,细胞的排列都很稀疏,所以采样率是很低的,然而在那里却也没有发生锯齿,原因就是通过细胞的不均匀分布来避免这个区域发生锯齿。

已经有人过研究眼睛中视锥细胞的分布,与人眼相似,光感受器在猴子眼睛的中央窝外部的分布如图所示,这样一个分布称之为泊松圆盘分布:采样点随机分布在一定的范围内且任意两个采样点之间的距离不小于某个值。距离的最小值能限制噪声的数量,举个例子,胶片颗粒(Film Grain)就是随机分布的,如下图所示,但是没有像泊松圆盘分布一样有最小距离的限制,而是采用纯随机分布。造成的结果就是一些样本点会集中一些区域而在其它的某些区域留下大量空白,所以胶片(Film)没有锯齿,有噪声(Noise)存在。

一种简单的实现泊松圆盘分布的方法是:
(1)随机生成采样位置,如果随机生成的采样位置与已经选择过的距离小于一给定值,则丢弃它,至少采样区域满为止,采用这种方法可以创建一个查询表(Lookup Table);
(2)还需要计算滤波器的值,该值描述了每个采样点与周围的像素点的关系。位置信息和滤波器的值存储在一个查询表中,这种简单的方法确实能产生很好的图像效果,但是要求有一个非常大的查询表。因此这里引入另外一种技术:抖动(Jittered)。
4.1.2 抖动采样(Jitter Sampling)
抖动采样其实是分层采样(Stratified Sampling)的一种,也时随机采样的一种形式,是一种逼近泊松圆盘分布的技术。
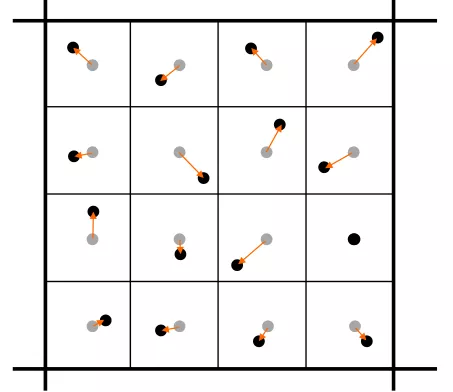
抖动技术又有很多种类型,这里主要介绍规格网格的抖动技术,这种技术能产生较好的实验结果并且很适用于图像渲染算法。其具体原理是对于每一个像素进行分割,并对于每一块的中心区域增加一个随机的偏移,保证偏移在同一块像素里。当然这种的采样方式也可用在对区域光的采样当中。
抖动可以使得高频信号降低,但是降低的高频信号中的能量会出现在噪声中而不会消失,因此基本的光谱组合没有发生变化。与纯种的泊松圆盘分布技术相比,该技术可能会造成更多的噪声,而且可能会留下部分锯齿。
分布式光线追踪随机采样模式的一个有趣的副作用是它们实际上将噪点注入到解决方案中(略微更粗糙的图像)。这种噪点比失真的图像更容易接受吧。
举个抖动的例子,计算时间抖动(Time Jitter)的效果,第n个样本抖动ζn的量,所以会在nT+ζn的位置采样,T表示采样周期,如下图所示,就是时间抖动的效果。可以采用不同的模型来表示抖动量ζn,比如用方差是σ2的高斯分布函数,增益量就可以为频率μ的函数,如下等式所示:
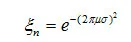

把一个像素看成是一个网格,或者由多个子像素(subpixel)网格构成的大网格,这样就是一个二维的抖动。噪声随机的加到X方向上的位置或者Y方向上的位置,X、Y方向相互独立,就相当于是两个一维的抖动构成的,要求使得每个采样点发生在某个像素网格范围内的随机位置上。如果已知道哪些采样点是可见的,则通过重构过滤器(Reconstruction Filter)对那些采样点的值进行处理。
重构过滤器的实现方法是一个开放性的问题,最简单的重构过滤器是箱式滤波器(Box Filter):取多个采样点的平均值。也可以采用加权重构滤波器,这种情况下,滤波器是一个采样位置与周围像素相关的加权值。每个像素是附近采样点的值乘以加权值的总和,这些滤波器可以提前计算好保存在一个查询表中。
抖动采样性能和方差的分析本篇文章篇幅问题暂时不予讨论,等有空的时候我们再一探究竟。
4.2 区域光和软阴影
Whitted光线追踪中的阴影是离散的。着色点时,检查每个光源以查看它是否可见。如果光源是可见的,则它对点的着色有贡献,否则它没有。光源本身由单个表示。

这对于距离很远的光源而言,这是相当准确的,但对于大型光源或近距离的光源来说,这个表示很差。这种离散决策的结果是阴影的边缘非常清晰。从点到可见光点到光源点都有明显的过渡。现实世界中的阴影要柔和得多。从完全阴影到部分阴影的过渡是渐进的。这是由于真实光源的有限区域和其他表面的光的散射。
分布式光线追踪尝试通过将光源表示为球和在球体表面的随机分布的点(区域光)来近似软阴影。当查看点是否处于阴影中时,围绕光源的投影区域投射一组光线。从光源传输到该点的光量可以通过击中光源的光线数量与投射的光线数量之比来近似。

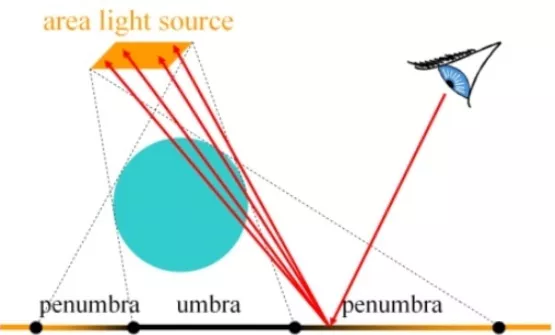
区域光源会产生柔和的阴影(Soft shadow = umbra +penumbra)也就是完全阴影和完全光照之间的区域,软阴影可以通过向区域光源表面上的随机点发射阴影光线来计算。
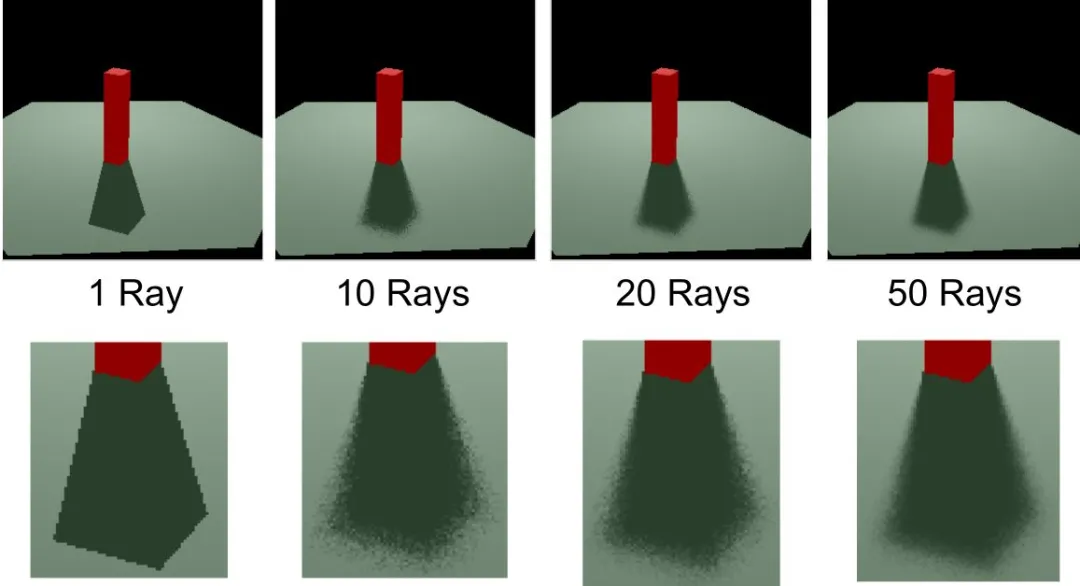
4.3 高光反射
Whitted光线追踪可以很好地表示完美的反射表面,但却难以表现出高光或部分反射的表面。只有当曲面是完美的镜子时,它的反射才看起来与现实完全相同。更常见的是表面是高光的并且反映了场景的模糊图像。这是由于表面的光散射特性。而传统的Whitted追踪中的反射始终是锐利的。

为什么呢,主要是由于,传统的光线追踪的反射的贡献,都只来自于其单一的反射向量。
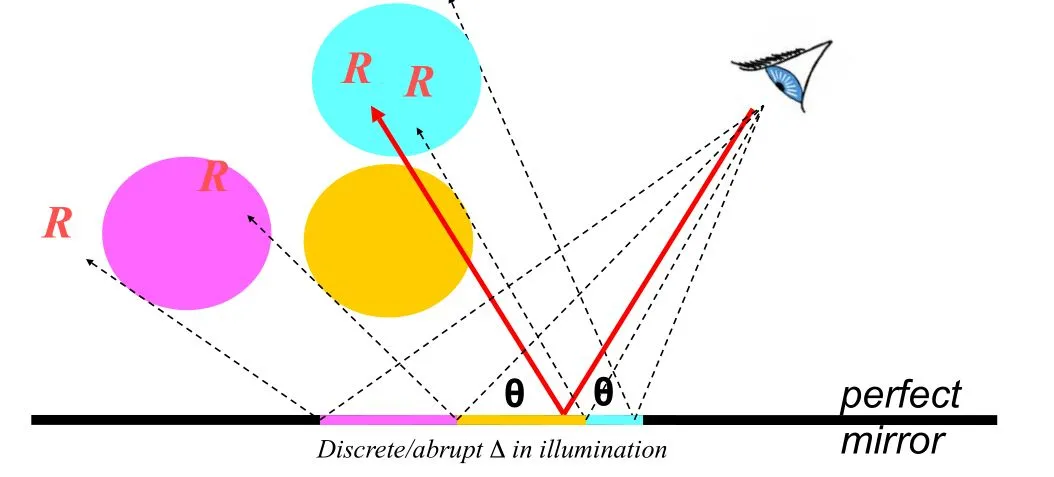
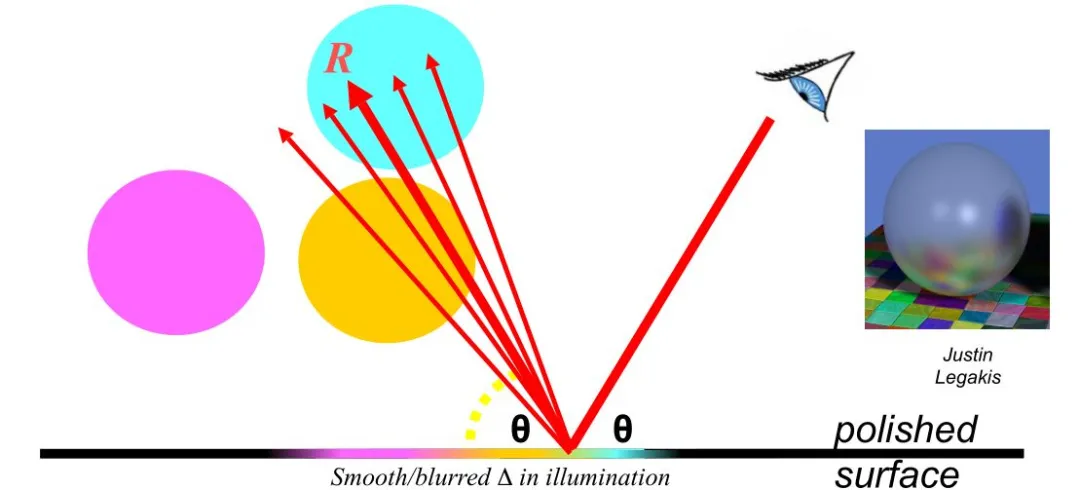
而分布式光线追踪的反射的贡献,不是沿反射方向投射单个光线,而是围绕反射方向发出一束光线,其是随机在锥体内对镜面角度周围进行多条光线采样。反射的实际贡献值可以通过取每个射线返回的值的统计平均值来得到。此方法还可用于通过使用区域光源生成镜面反射高光。如果从表面反射的光线撞击光源,它们将添加到表面照明的镜面反射分量。这可以取代phong模型的镜面反射分量。并且,反射强度随着镜面角度缩小迅速下降,该方向的取样概率应同样下降。

4.4 透明度 Transparency
Whitte光线追踪可以很好地表现出完美透明的表面,但是在表现半透明的表面方面很差。半透明的真实表面通常传输其后面的场景的模糊图像。分布式光线追踪通过在传统光线追踪的折射光线的大致方向上投射随机分布的光线来实现这种类型的半透明表面。然后将从这些射线中的每一个计算的值平均以形成真正的半透明分量。
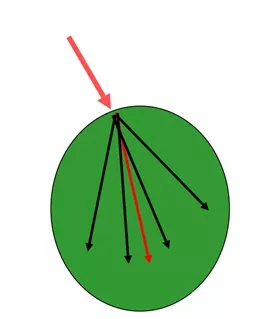
基本的Monte Carlo光线追踪方法效率不高,主要原因是会出现多次反射,折射却打不到光源的情况,特别是在光源面积比较小的地方非常明显。我们可以通过对光源进行采样来解决这个问题。在每次射线打到物体得到交点后,我们可以在面光源上采一个点,然后判断连接交点和光源点的阴影线是否被遮挡,如果未被遮挡,则可以计算光源对物体表面交点的直接光照。在这个过程中要通过使用多重重要性抽样(Multiple Importance Sampling)[4] 计算这次反射的pdf。

4.5 动态模糊(Motion Blur)
在摄像机中,快门速度表示每帧表示在相机快门打开期间场景的时间。如果场景中的物体相对于相机处于运动状态,则它们将在胶片上显得模糊。这个原理是常识性的,拍摄飞奔的运动员时,你需要较快的快门速度,否则由于曝光时间过长,图片会变的不清晰,因为最终的像素是这一时间曝光得到的平均值。当然如果你要的效果就是那种夜间川流不息的车辆的灯光流尾的效果,就需要比较长的快门速度,这还需要三脚架等固定工具,因为手抖会造成周围的景致的物体模糊。
分布式光线追踪可以通过在时间上和空间上分布光线来模拟这种模糊。在投射每条光线之前,将对象平移或旋转到该帧的正确位置。然后对光线进行平均后得到实际值。运动最多的对象在渲染图像中的模糊程度最高。这其实就是对时间的采样平均。

4.6 景深(depth of field)
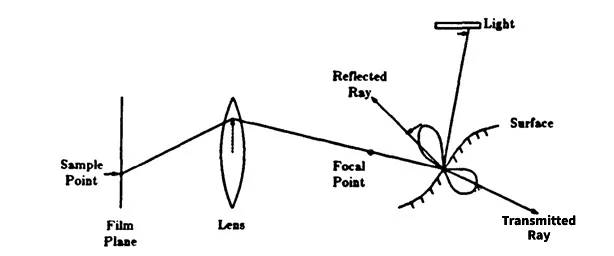
人眼和相机都具有有限的镜头光圈,因此具有有限的景深。两个远处或两个近处的物体将显得不聚焦且模糊。但是几乎所有计算机图形渲染技术都使用针孔相机模型。在此模型中,无论距离如何,所有对象都处于完美的焦点。在许多方面,这是有利的,由于缺乏聚焦而导致的模糊通常在图像中是不希望的。然而,模拟景深可以产生更逼真的图像,因为它可以更准确地模拟真实的光学系统。
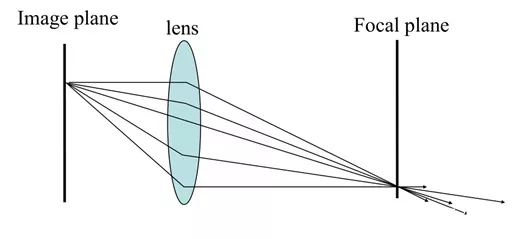
分布式光线追踪通过在视平面(Image plane)前放置人造透镜(Lens)来创建景深。再次使用随机分布的光线来模拟景深的模糊。第一次射线投射不会被镜头修改。假设透镜的焦点沿着该光线处于固定距离处。发送给同一像素的其余光线将散射在镜头表面周围。在镜头处,它们将弯曲以穿过焦点。场景中靠近镜头焦点的点将清晰对焦。更近或更远的点将变得模糊。

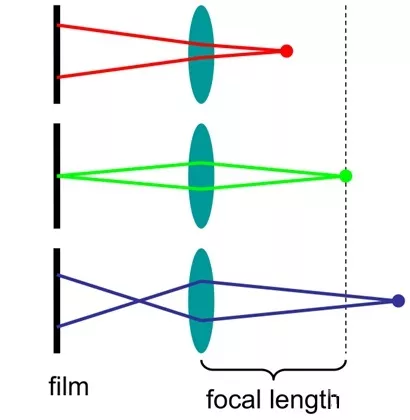
在所有在focal length里面的物体都是清晰的,其它的物体会变模糊。
4.7 分布式光线追踪的缺点
它的主要问题在于分布式光线追踪指数性质。你首先会发射光线,这通常是最重要和最重要的照明贡献。但是对于次级反弹,你必须发射越来越多的光线。1射线变成10射线,每射出10,你有100射线,每射出10,你有1000,依此类推。所以你的第3次反弹需要多1000倍的阴影,即使它可能占最终照明的1/100或更少。
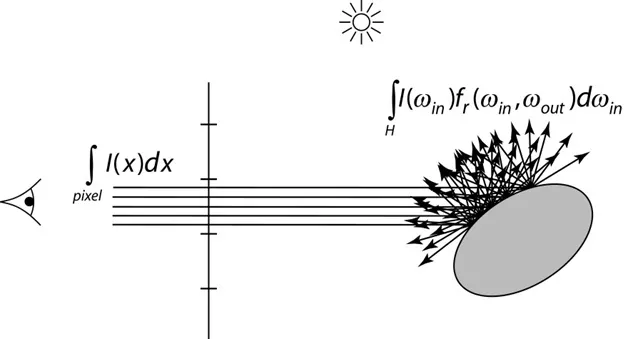
如上图,如果像素抗锯齿+反射抗锯齿,想想都可怕。它本质上是低效率的,因为你花费最多的时间来计算图像中最不重要的部分。高级照明效果(如焦散)也很难使用分布式光线光线追踪进行渲染。
五.路径追踪
当Kajiya在1986年提出渲染方程时,他也给出了解决这个方程的方法。Kajiya将渲染方程转换为一个基于路径积分的形式。
路径追踪是分布式光线追踪的一种变体,其中每个点只发出一条反射和折射光线。这样可以避免光线数量的激增,但太简单的实现会导致拥有非常多噪点的图像。为了弥补这一点,每个像素都对多条光线进行追踪。
路径追踪的一个优点是,由于每个像素发出较多的可见性光线,因此可以以很少的额外成本合并景深和运动模糊等相机效果。另一方面,与分布式光线追踪相比,要确保反射光线(例如通过分层)的良好分布更为困难。简而言之,分布式光线追踪在光线树中发出的光线最多,而路径追踪追踪在初始时发出的光线最多。
5.1 路径追踪方程
渲染方程有两种形式,第一个就是我们经常使用的半球面形式,但是它还有一个重要的形式,那就是面积形式。Kajiya将渲染方程转换基于路径积分的显式方程,光照计算才能有效的进行蒙特卡洛计算。
根据立体角微元和面积微元间的关系:
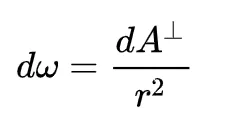
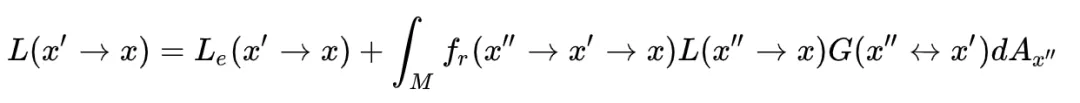
这就是最终的面积积分形式,不停的进行左右替换,就得到了这样一个和式:
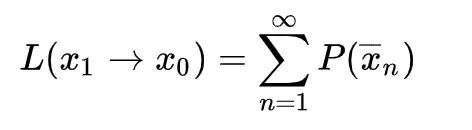
其中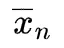 指长度为n的路径
指长度为n的路径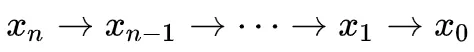 ,
, 是光源经n段传播过程后为最终结果作出的贡献:
是光源经n段传播过程后为最终结果作出的贡献:
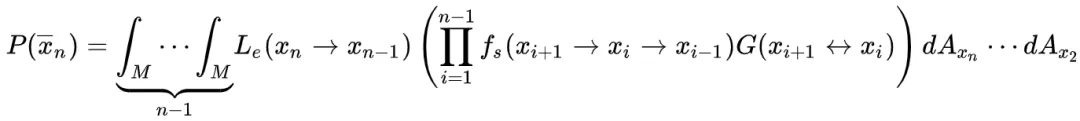
这就是LTE的路径和形式。这是一个n-1维的高维积分,我们之后每一个采样样本都是一个n-1维的向量。我们称这个向量所在的空间为路径空间。
路径积分形式的好处是它把对整个场景的渲染问题转化成了对一个对由各种长度路径组成的路径空间的采样问题。在视点和光源之间随机生成若干条路径,估计它们的贡献值,并把贡献值加到该路径影响到的像素上,就可以得到场景的渲染图像。双向路径追踪和Metropolis光线追踪都很适合采用这种路径积分形式来描述和计算。

5.2 直接照明
5.2.1 只有一盏灯的照明
由于要计算灯光,所以 我们需要把半球积分变为面积积分:
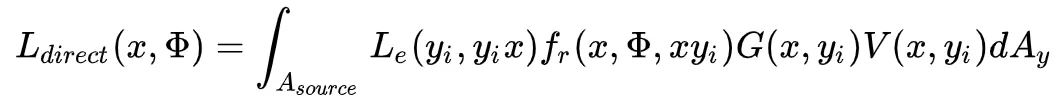
其中 yi 是在灯光范围上的点, V(x,y)是阴影光线的可见函数,有遮挡物时为1,否则为0。
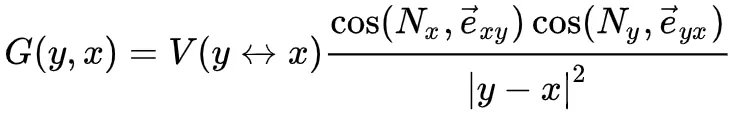
为了计算由于场景中的单个光源(引起的直接照明,我们需要在光源的区域上定义概率密度函数 p(y) ,在上面会产生阴影射线。我们假设可以构造这样的PDF,而不管光源的几何特性。我们使用蒙特卡洛积分进行估计。
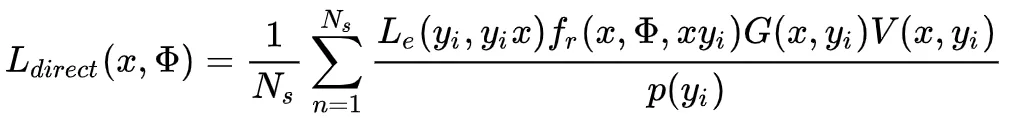
directIllumination (x, theta)//x是表面的点
estimatedRadiance = 0;
for all shadow rays
generate point y on light source;
estimatedRadiance +=Le(y, yx) * BRDF * radianceTransfer(x,y)/pdf(y);
estimatedRadiance = estimatedRadiance / #shadowRays;
return(estimatedRadiance);
蒙特卡罗积分的方差以及最终图像中的噪点,主要由 p(y) 的选择决定。理想情况下 p(y) ,等于每个点 y 对最终估计量的贡献,但实际中,这几乎是不可能的,必须进行更实际的选择,主要是易于实现。p(y) 的经常使用的选择是:
- 光源区域的均匀采样
- 光源对立体角的均匀采样
光源区域的均匀采样
在这种情况下,p(y) 是均匀的分布在灯光的表面,所以每一个点的概率是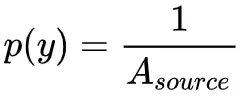 。这是对光源进行采样的最简单方法,并且可以轻松使用分层采样等优化方法进行改进。使用这个采样方案,图像中会有几个噪声源。如果一个点 x 位于阴影的半影区域,它的一些阴影光线将产生V(x,yi)=0 ,而有些则不会。这会导致在软阴影区域内产生大部分噪点。另一方面,如果在阴影外,大部分噪点都是由余弦项的变化引起的。
。这是对光源进行采样的最简单方法,并且可以轻松使用分层采样等优化方法进行改进。使用这个采样方案,图像中会有几个噪声源。如果一个点 x 位于阴影的半影区域,它的一些阴影光线将产生V(x,yi)=0 ,而有些则不会。这会导致在软阴影区域内产生大部分噪点。另一方面,如果在阴影外,大部分噪点都是由余弦项的变化引起的。
光源对立体角的均匀采样
为了消除由余弦项和平方因子引起的噪声,可选择根据立体角进行采样。这需要将光源区域上的积分重写为光源所对的立体角上的积分。这将从被积函数中去掉一个余弦项和距离因子。但是,可见性测试仍然存在。这种采样技术通常很难实现,因为在任意立体角上生成方向并不简单。
5.2.1 多盏灯的照明
当场景中有多个光源时,最简单的方法是依次为每个光源分别计算直接照明。我们为每个光源生成一些阴影光线,然后总结每个光源的总贡献。这样,每个光源的直接照明分量将独立地计算,并且可以根据任何标准选择每个光源的阴影射线的数量。
但是,通常最好将所有组合光源视为单个,并将蒙特卡罗积分应用于组合积分。当产生阴影射线时,它们可以被任何光源使用。因此,可以仅用单个阴影射线计算任意数量光源的直接照射,并且仍然可以获得无偏图像(尽管在这种情况下,最终图像中的噪声可能非常高)。这种方法之所以有效,是因为我们将光源完全抽象为单独的解析曲面,只需查看一个集合。然而,为了获得能工作的算法,我们仍然需要单独访问任何光源,因为任何单独的光源可能需要单独的采样程序来在其表面上生成点。
5.3 间接光照
与直接照明计算相反,间接光照这个问题通常要困难得多,因为间接光从所有可能的方向到达表面点。因此,很难按照与直接照明相同的路线优化间接照明计算。
间接照明包括在光源和x之间的中间表面上至少反射一次后到达目标点X的光。间接照明是全局光照的一个非常重要的组成部分。
indirectIllumination (x, theta)
estimatedRadiance = 0;
if (no absorption)
for all indirect paths
sample direction psi on hemisphere;
y = trace(x, psi);
estimated radiance +=computeRadiance(y, -psi) * BRDF *cos(Nx, psi) / pdf(psi);
estimatedRadiance = estimatedRadiance / #paths;
return(estimatedRadiance/(1-absorption));
computeRadiance(x, dir)
estimatedRadiance = Le(x, dir);
estimatedRadiance += directIllumination(x, dir);
estimatedRadiance += indirectIllumination(x, dir);
return(estimatedRadiance);
5.3.1 间接光的均匀采样
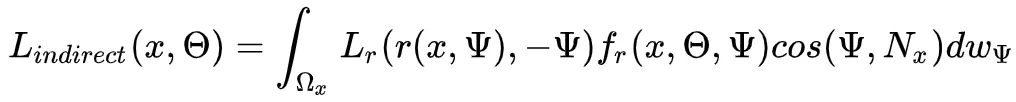
评估间接照明的最一般的蒙特卡罗方法是使用任意的半球PDF, ,并生成n个随机方向的
,并生成n个随机方向的 。这将产生以下估计量:
。这将产生以下估计量:
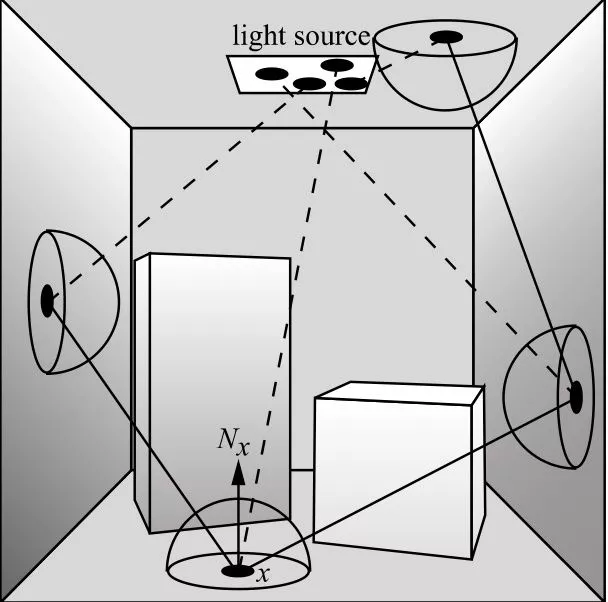
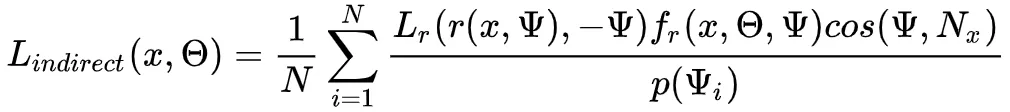
为了计算这个估计量,对于每个生成的方向,我们需要评估沿着 方向从 x 追踪一条射线的BRDF和他的余弦项,并评估最近交
方向从 x 追踪一条射线的BRDF和他的余弦项,并评估最近交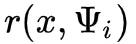 处的反射辐射度
处的反射辐射度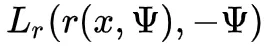 。最后这个值表面了间接照明的递归性质,因为
。最后这个值表面了间接照明的递归性质,因为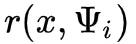 处的反射辐射可以再次分解为直接和间接贡献。这里直接给出均匀采样的PDF,为
处的反射辐射可以再次分解为直接和间接贡献。这里直接给出均匀采样的PDF,为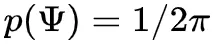 。所产生的图像中的噪点主要将由BRDF和余弦项的评估变化以及远点处的反射辐射 Lr 的变化引起。
。所产生的图像中的噪点主要将由BRDF和余弦项的评估变化以及远点处的反射辐射 Lr 的变化引起。
5.3.2 间接光的重要性采样
在半球上进行均匀采样是一种非常鲁莽的决策,因为这显得好像我们对间接照明积分中的被积函数没有任何了解。为了降低噪点,我们需要某种形式的重要性采样。我们可以构造一个与以下任何因素成比例(或近似成比例)的半球形PDF:
- 余弦项
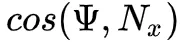
- BRDF
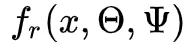
- 间接辐射度

- 上面任何形式的结合
余弦项采样
与法线 Nx 周围的余弦波成比例的采样可防止在半球的水平线附近采样过多,其中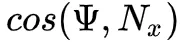 等于0。我们可以预期噪点最终会减小,因为我们降低了概率对生成的方向贡献很小的方向。所以:
等于0。我们可以预期噪点最终会减小,因为我们降低了概率对生成的方向贡献很小的方向。所以:
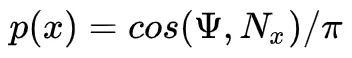
假设BRDF在此点只有漫反射,我们可以得到:
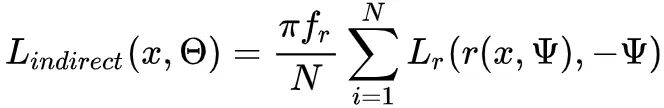
这里,唯一的噪点来自于 Lr 。
BRDF采样
有些材料仅在非常特定的方向上反射光。这通常与材料的粗糙度有关。镜子(例如左边的镜子)需要的样本比右边的漫反射表面少得多。

这取决于材料的双向反射分布函数(BRDF)。该分布函数决定了在给定方向上反射的光量。通过采样方向直接从该分布函数(重要性采样)进行测试,我们可以避免采集对最终图像贡献很小的样本。
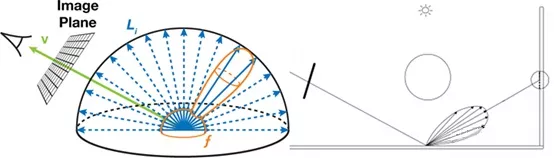
BRDF采样是一种很好的降噪技术,当有光泽或高镜面BRDF时。它降低了在BRDF值较低或为零时对方向进行采样的概率。然而,只有少数的特定的BRDF模型才有可能精确地按照BRDF比例采样。更好的办法是,试着按照BRDF和Cosine项的乘积比例取样。从分析上讲,这更难做到,除非在少数情况下。通常,根据这种PDF,需要结合拒绝进行抽样。
另一种耗时的方法是建立一个累积概率函数的数值表,并使用该表生成方向。PDF值并不完全等于BRDF和Cosine因子的乘积,但仍然可以实现显著的方差减少。说明按照BRDF采样,让我们考虑修改后的Phong BRDF。
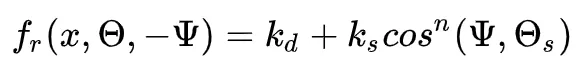
这里 d 的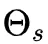 是完美的镜面反射方向。
是完美的镜面反射方向。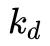 是漫反射部分,
是漫反射部分,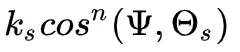 是高光部分,所以间接光部分我们可以分为:
是高光部分,所以间接光部分我们可以分为:

对于一个点来说,我们进行的是分类讨论,发生漫反射的比例为q1。

发生高光的比例q2。

发生吸收的比例q3,贡献值为0。
q1+q2+q3=1
对于漫反射部分,我们比较好的选择是根据余弦分布,高光部分可以根据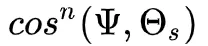 。
。
另外,q1、q2、q3的值也会也会影响最后的结果,原则上,不管选择哪一组值最终都会提供一个无偏估计量,但是仔细选择这些值会对最终结果产生影响。一个好的选择是选择与不同模式中的(最大)反射能量成比例的这些值。这些值可以通过对沿表面法线 Nx 的入射方向的反射进行积分来计算:
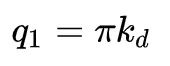

需要注意的是,对于除法线之外的任何其他入射方向,q的值实际上大于实际反射能量,因为围绕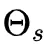 的余弦波部分位于x处的表面下方。这可以通过不重新采样位于波形下方的波形部分中的任何方向来调整,从而保持在漫射能量,镜面能量和吸收之间取得平衡。
的余弦波部分位于x处的表面下方。这可以通过不重新采样位于波形下方的波形部分中的任何方向来调整,从而保持在漫射能量,镜面能量和吸收之间取得平衡。
5.4 完整的算法
computeImage(eye)
for each pixel
radiance = 0;
H = integral(h(p));
for each sample // Np viewing rays
pick sample point p within support of h;
construct ray at eye, direction p-eye;
radiance = radiance + rad(ray)*h(p);
radiance = radiance/(#samples*H);
rad(ray)
find closest intersection point x of ray with scene;
return(Le(x,eye-x) + computeRadiance(x, eye-x));
computeRadiance(x, dir)
estimatedRadiance += directIllumination(x, dir);
estimatedRadiance += indirectIllumination(x, dir);
return(estimatedRadiance);
directIllumination (x, theta)
estimatedRadiance = 0;
for all shadow rays // Nd shadow rays
select light source k;
sample point y on light source k;
estimated radiance +=Le * BRDF * radianceTransfer(x,y)/(pdf(k)pdf(y|k));
estimatedRadiance = estimatedRadiance / #paths;
return(estimatedRadiance);
indirectIllumination (x, theta)
estimatedRadiance = 0;
if (no absorption) // Russian roulette
for all indirect paths // Ni indirect rays
sample direction psi on hemisphere;
y = trace(x, psi);
estimatedRadiance +=compute_radiance(y, -psi) * BRDF *cos(Nx, psi)/pdf(psi);
estimatedRadiance = estimatedRadiance / #paths;
return(estimatedRadiance/(1-absorption));
radianceTransfer(x,y)
transfer = G(x,y)*V(x,y);
return(transfer);。
路径追踪适用于任何类型的几何图形,任何类型的BRDF,采样所有类型的路径,内存消耗低,但是其最大的问题就是标准的蒙特卡洛问题:慢收敛,和噪点。
缺点也是很明显的,首先效果上因为取巧不如分布式光线追踪,然而纯路径追踪的收敛速度是很慢的,从视点打出的光线有的时候很难找到一条贡献大的路径(即找到这样一条路径的概率很小),造成图像往往有很多噪点,每个像素需要上千个采样才能达到满意的效果。
关于俄罗斯轮盘赌就是不能简单的固定步长的终止追踪,因为贡献度高的应该长度越长,低的就越短。主要也是能量守恒。这个网上比较多,不说了。
六.双向路径追踪
双向路径追踪算法,是由Veach和Guibas和Lafortune和Willems分别提出的,它可以很好的生成焦散和镜面。
双向路径追踪(Bidirectional Path Tracing)的基本思想是同时从视点、光源打出射线,经过若干次反弹后,将视点子路径(eye path)和光源子路径(light path)上的顶点连接起来(连接时需要测试可见性),以快速产生很多路径。
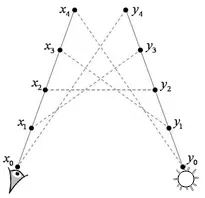
从眼睛生成长度为nE的子路径:x1、x2、x3、x4...,从光源生成nL条子路径,y0、y1...。然后,我们分别连接这两条子路径上的每个结点,只有两个位于两条子路径上不被其他物体遮挡的结点才可以连接。这样,我们可以得到不同长度的一组路径,而且这组中相同长度的路径有多条。例如我们要得到一条长度为 k 的路径,我们可以从光源子路径中选择长度为 s 的路径然后从眼睛子路径中选择长度为 t(t=k+1) 的路径,所以对于长度为 k 的路径,我们可以有k种选择,每一种 s 的选择, 实际上就代表了一种不同的对路径空间的采样策略,这些策略每一种都有它适用的情况,对于产生某种特殊的效果产生各自的作用,将这些策略综合起来,我们就可以得到适应性更强的渲染算法,得到更好的渲染效果。这些策略大体上可以分为三类,
s = 0,例如 x0、x1...xk这种情况是基本的Monte Carlo光线追踪,也就是在生成眼睛子路径的过程中打到了光源。
t=1,例如 x0(E)↔yk-1y0(L) 这种情况是光源光线追踪,直接连接视点和光源子路径。这条路径影响到的像素不是最初的像素,必须通过计算得到,而且需要注意眼睛和光源子路径的端点是否可见。另外,这里 t≠0 ,因为在这里我们不考虑视点有一定面积的情况,而把视点看作是一个抽象的点。
S=1,…k,例如,x0(E)x1...xi↔yk-i-1y0(L),这是一般的情况,需要注意互联的两个点是否可见。
[Veach 1995]提出了多重重要性采样(Multiple Importance Sampling)的方法,可以将各种采样方法采样的结果以合适的权重合并起来,非常有效地降低图像的噪声。比如,现在要求解积分中所有长度为 4 的光路的贡献,可以有以下几种采样方法:视点子路径长度为 0, 光源子路径长度为 3,记为(0,3);和(1,2),(2,1),(3,0)。这些方法采样出来的路径贡献可能相差很大,使用多重重要性采样合并这些采样可以达到很好的降噪效果。然而双向路径追踪也有明显的缺点,当两个顶点都在纯镜面或折射面上时,双向路径追踪方法不会去连接这两个顶点,这样就造成了它难以有效地模拟Caustics的反射和折射。
Choose a light ray from the light//从光源选择一条光线
Find ray-surface intersection//找到光线和物体表面的交点
Reflect or transmit//进行反射或者折射
u = Uniform()
if u < reflectance(x)
Choose new direction d drawn from BRDF(O|l)/
Goto 2/根据BRDF找到新的方向进行反射
else if u < reflectance(x) + transmittance(x)
Choose new direction d drawn from BTDF(O|l)
Goto 2/根据BRDF找到新的方向进行反射
七.Metropolis 光线追踪
路径追踪(Path Tracing)中一个核心问题就是怎样去尽可能多的采样一些贡献大的路径,Eric Veach等人于1997年提出了梅特波利斯光照传输(Metropolis Light Transport,常被简称为MLT)方法。
1953年,Metropolis等人为了解决计算物理领域的复杂采样问题,提出了一种新的采样方法,这就是Metropolis方法。他们最早使用Metropolis方法的初衷是为了计算流体的材质属性,现在,Metropolis方法已经在物理、化学等很多领域得到了广泛的应用。同样,我们也可以将Metropolis方法应用在全局光照领域,来解决复杂的采样问题。之前的这些光线追踪的算法最大的问题是它们都有不适和的场景,也就是说没有一种方法对任意场景都起作用,因为这些方法对场景中从光源到视点的路径进行采样时都没有考虑到场景的路径分布特征,都是采用随机采样的方法采样路径并计算贡献。因此,一旦场景的路径空间中路径分布极不均匀,这些方法就会因为大量的路径没有带来贡献而造成效率的极度降低,例如在间接光照主导的场景中,光源和视点之间被严重遮挡,只有很小的通道可以通过,随机采样时,只有很少的路径可以通过这个通道带来贡献,其它的路径只能被丢弃。
重要性采样的选取需要样本与函数 f 成比例,即采样样本要成比例于函数 f 的概率分布。而在实际无偏的渲染过程中,函数 f 为已知函数,但由于其形式较为复杂和不规则,采样过程中样本的选取所形成的概率分布很难成比例于函数 f ,这样就会导致样本的方差较大。Metropolis提出了一种方法可以生成采样,样本的概率分布可以成比例于任何可以估计的函数。
样本由马尔可夫链生成,所以每一个样本只与其前一个样本相关而与其他样本无关。新生成的样本由当前样本随机突变生成,其突变过程满足设定的突变策略。突变策略的选取较为开放,但是其需要满足遍历性。遍历性指采样过程中,无论从任何初始样本开始采样,最终采样过程都将逐渐的收敛于 pi 的分布。
采样分布的获得是通过对突变样本的接收和拒绝实现的,最终样本的接收和拒绝取决于接收概率的设置。接收概率表示接收突变样本 y 为当前样本 x 的概率表示为 a(y|x)。最终马尔可夫过程将收敛至一个平稳分布,若此过程处于平稳状态,空间中两个样本的转移密度也处于平稳状态。这种性质被称作细节平衡条件。
当接收概率满足细节平衡条件,突变策略满足遍历性,生成采样序列的概率密度将服从平稳分布。为了尽快使采样过程收敛达到平稳分布,将接收概率设置得尽可能大是一种较好的策略。
7.1 马尔科夫链
7.1.1 概念
X是一个随机变量,其可能的取值来自于集合 ,X在离散时刻 t的取值为Xt ,若 X 随时间变化的转移概率仅仅依赖于其当前时刻的取值Xt ,即
,X在离散时刻 t的取值为Xt ,若 X 随时间变化的转移概率仅仅依赖于其当前时刻的取值Xt ,即
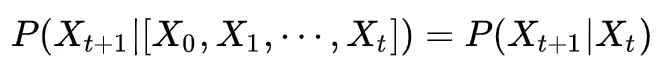
那么随机变量X随时间变化的过程是一个马尔科夫过程X在 [0,t] 时间内随时间变化生成的序列(X0、X1、...、Xt)就是一个马尔科夫链。
7.1.2 转移概率矩阵
设随机变量X在任意时刻t+1的取值为si的概率为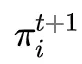 ,即
,即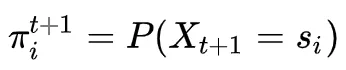 ,其中t为一个任意时刻。随机变量从状态 sj 转移到状态 si 的转移概率为Pji:
,其中t为一个任意时刻。随机变量从状态 sj 转移到状态 si 的转移概率为Pji:

t 为任意时刻,那么我们可以得到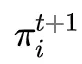 的计算公式如下:
的计算公式如下:
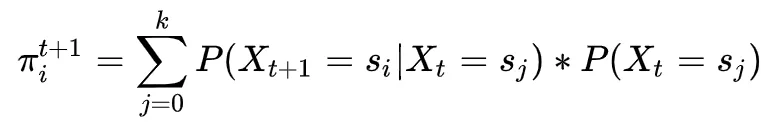
我们注意到在上式中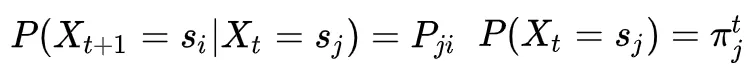 ,因此上式可以写成以下形式:
,因此上式可以写成以下形式:
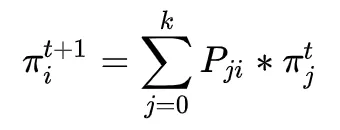
那么我们可以将随机变量X在t+1时刻取值为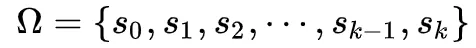 的概率写为如下形式:
的概率写为如下形式:
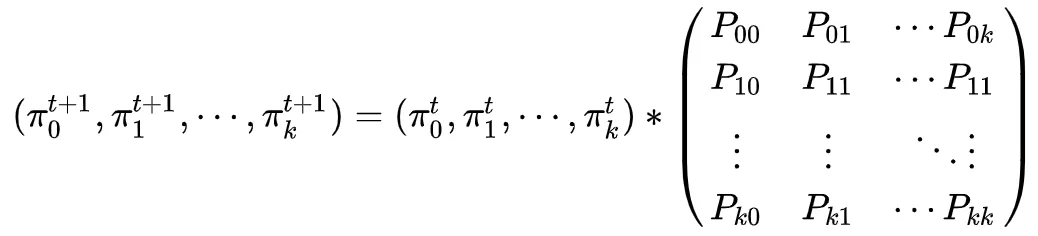
将上式右侧的矩阵记为Ptran,即:
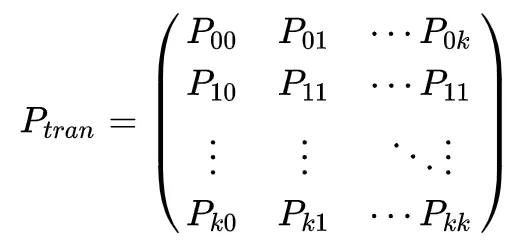
Ptran就是马尔科夫过程的转移概率矩阵。
7.1.3 平稳分布
如果一个马尔科夫过程的某个状态经过有限次状态转移后又回到自身,那么我们称这个马尔科夫过程具有周期性。如果一个马尔科夫过程存在两个状态,它们之间是互相转移的,那么我们称这个马尔科夫过程可约。若一个马尔科夫过程既没有周期性又不可约,那么这个马尔科夫过程是各态遍历的。各态遍历这个概念我个人的理解是,每个状态都有一定的概率会出现。
各态遍历的马尔科夫过程有一个重要性质:无论初始的状态概率 取值如何,经过足够多次的状态转移,各态遍历的马尔科夫过程会趋于一个平稳分布
取值如何,经过足够多次的状态转移,各态遍历的马尔科夫过程会趋于一个平稳分布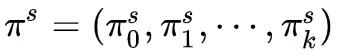 :
:
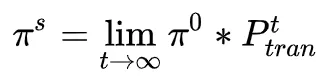
这时随机变量X从 取值的概率不再变化,而是服从平稳分布
取值的概率不再变化,而是服从平稳分布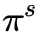 。
。
平稳分布满足性质: 即平稳分布经过状态转移后随机变量取值的概率不变,这是当然的。
即平稳分布经过状态转移后随机变量取值的概率不变,这是当然的。
这是侑虎科技第1065篇文章,感谢作者papalqi供稿。欢迎转发分享,未经作者授权请勿转载。如果您有任何独到的见解或者发现也欢迎联系我们,一起探讨。(QQ群:793972859)
作者主页:https://www.zhihu.com/people/papalqi,再次感谢papalqi的分享,如果您有任何独到的见解或者发现也欢迎联系我们,一起探讨。(QQ群:793972859)
完整内容可前往此处查看。