基于屏幕空间渲染的液体模拟

本文介绍一种液体粒子模拟的屏幕空间渲染（Screen Space Fluid Rendering, 简称SSF）方法。这种方法没有Mesh重建的过程，实现简单而高效，在游戏等对实时性有严格要求的领域中有广泛的应用前景。

几天前看到了西半球饭桶实现的基于位置的流体（Position Based Fluids）https://www.zhihu.com/question/275611095/answer/414977450
原答案没有做粒子液体的表面的重建。恰巧我最近以学习管线渲染和初尝模拟算法为契机，也对这篇论文做了复现，本文是对粒子模拟渲染部分的补充。

传统方法

计算机图形学中，欧式网格和拉氏粒子是两种主要的流体离散方法。无论是哪一种方法，都需要先重建液体表面，再进行渲染着色，以得到最终图像。(液体外的其他流体各有渲染方法，如渲染烟雾可用体渲染。在此不谈)

液体表面重建，直到近几年以前，一直是移动立方体方法（Marching Cubes）的天下。移动立方体法发表距今已经有30年了。这种方法使用了水平集（Level Set）的思想（水平集可以理解为高维上的等高线），将液体表面定义为液体密度等于某个小常数C的点集。Marching Cubes方法将空间离散为等大的立方体网格，检查每个网格上8个顶点的液体密度情况。

论文中的15种顶点和重建形态

若网格上一条边的两个端点密度值跨过阈值C，则算法认为这条边上存在一个表面Mesh的顶点。上图中，被标记的顶点密度大于C，否则小于C。将每个网格构造的多边形拼接，即可得到整个液体表面的Mesh。油管上有一个很棒的演示动画：
https://www.youtube.com/watch?v=B_xk71YopsA
把构造表面的过程可视化为一个立方体在空间中扫描的过程。可以理解算法名字中“移动（Marching）”一词的来历。

欧式流体天生就是网格模拟，可以直接应用Marching Cubes。对粒子形态的拉式流体，空间中一点的密度是通过周围粒子携带的密度值计算得到的。最常使用的SPH方法将粒子表达为有限半径空间内的质量分布：

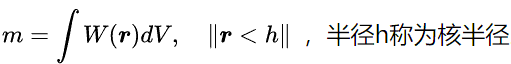
图片来源Neutrino-SPH Dynamic Simulation System

直接使用SPH计算密度重建得到的液体表面会有很强的粒子感。Adam等人提出使用流体的局部区域信息重构粒子数量和大小，Yu等人提出使用在液体不同区域使用椭球形的粒子替代球形粒子，都取得了很好的重建效果。可以看到，液体平静的表面基本不再有粒子状的伪像（artifact），浪尖等细节处也被还原得更加精细。

左：球形粒子，右上：Adam，右下： Yu

屏幕空间渲染

传统方法的效果优良，但是实现麻烦，复杂度高。例如Yu的方法，不仅使用了PCA处理粒子形状的变换矩阵，还需要为渲染重建一次邻居搜索哈希网格，代价比较高昂。

屏幕空间渲染（Screen Space Fluid Rendering, 简称SSF）则给出了粒子渲染的一种新思路。这个算法不涉及液体网格表面的匹配和重建，实现相对简单得多。在不追求全局光照的实时管线渲染应用中，它的效果还比较令人满意。这个算法也是Position Based Fluids原论文中使用的渲染算法。

粗略地讲，屏幕空间渲染首先利用Point Sprite渲染粒子，将液体在屏幕空间的深度和厚度记录在两张二维纹理上。深度纹理记录了屏幕上某点的液体表面到摄像机的距离，厚度纹理记录了表面之下液体的厚度。然后对深度纹理进行平滑，并从平滑后的深度纹理中还原表面法线。得到法线后便可以计算反射/折射，对表面进行最终的着色了。

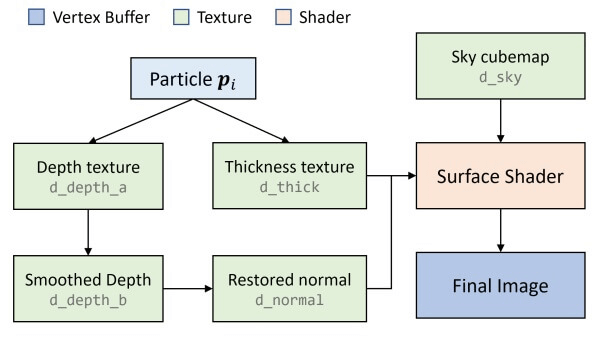
渲染用纹理和流程

深度纹理

深度纹理是整个算法的核心。深度指的是液体表面到摄像机的距离。我们使用的是Y轴向上的摄像机，则深度可以认为是被渲染物理的Z坐标。渲染时，开启深度测试，这样我们就能保证处于表面的粒子覆盖内部的粒子。

深度纹理，越白距离摄像机越远

深度纹理是使用Point Sprite渲染的。所谓Point Sprite，就是将粒子以Point形式渲染，这样会将粒子渲染成一个正方形。为了渲染成圆形，在Fragment Shader中读取PointCoord，Discard圆以外的像素即可。同时要注意以下两点：

• 要在Vertex Shader中根据粒子深度正确地计算并设置Point大小，以符合透视规律。
• 要反应球形粒子不同位置的深度差异，因此需要结合粒子位置和PointCoord计算深度值。

厚度纹理

厚度纹理记录了表面下液体的厚度。着色时考虑液体厚度，能够增加液体的层次感。根据Beer-Lambert定律，越厚的液体透光率越低。

厚度纹理，越白越厚

厚度纹理也是利用Point Sprite渲染的。与深度纹理一样，也需要根据粒子深度调整渲染Sprite的大小。不同的是，渲染时关闭深度测试，开启加法混合，从而使得重叠的粒子厚度能够叠加。同时，要根据PointCoord正确地计算每个像素的厚度值，反应球形粒子四周薄，中间厚的特点。

法线还原

得到深度纹理就可以还原表面法线了。法线储存在一张RGB三通道24bits的二维纹理上。

三维空间中的参数曲面：

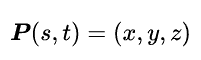
上一点的法向量可由公式给出：

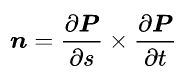
实际上，两个偏导给出了切平面上的两个不平行的向量，因此叉乘可以得到这个平面的法向量。纹理坐标就是曲面参数。已知摄像机参数，又可以从纹理坐标可以还原液体表面X，Y坐标，同时纹理中记录了Z坐标，因此可以利用公式计算法线。偏导使用使用一阶差分计算：

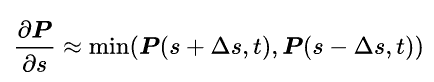
上面的近似取了前向差分和后向差分的较小值。这是因为深度纹理上有许多深度不连续的地方。使用单独使用前向或后向差分都会导致不正确的结果。

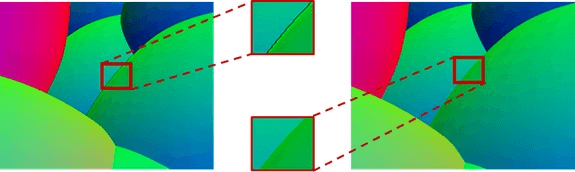
深度不连续处的差分处理
左：错误的法向量还原，右：正确的法向量还原

法向量重建结果。三维坐标映射到RGB

可以发现法线纹理的粒子形状分明。这当然不是我们所希望的。因此有必要先对深度纹理进行平滑，再从平滑后深度中重建法向量。

直接平滑法向量也是一种可行的做法。但因为粒子的深度信息未变，而计算着色时，需要使用粒子位置做光线追踪操作，因此会损失一些精确性。另外，因为法向量是三维的，而深度是标量，平滑法向量的计算量也比较大。

深度平滑

没平滑的直接渲染得到的画面会有很强的粒子感。

无平滑的最终渲染结果

我们可以使用双边滤波（Bilateral Filtering）先对深度纹理进行平滑。双边滤波可以很好保留深度的不连续性。其他一些模糊算法，例如高斯模糊，则会错误地把本在两个不同深度的表面模糊成一块。

平滑深度纹理
左：高斯模糊，右：双边滤波

双边滤波是一个复杂度为 O(r^2) 的算法，r是平滑半径。测试中发现，当r大于15个像素的时候，就会对实时性产生显著影响了。然而，粒子大小常常不止15像素。一种方法是，使用双边滤波算法的一次近似，下面链接中有描述。
http://developer.download.nvidia.com/presentations/2010/gdc/Direct3D_Effects.pdf但这种方法会带来一些Artifact。因此我采用的方法是使用小平滑半径平滑多次，从而以较小的复杂度近似达到大平滑半径的效果。

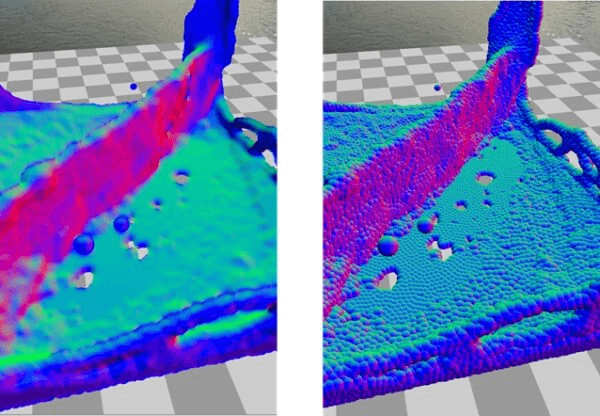
平滑后法线
左：平滑后，右：平滑前

表面着色

有了深度纹理，可以还原每个像素在摄像机空间的坐标。有了法向量纹理，可以计算着色。我们综合考虑液体表面的折射和反射，计算每个像素最终的颜色。

光线在液体表面的传播情况

首先我们可以计算表面的折射方向和反射方向，并通过反向追踪光线，得到折射光和反射光的颜色。下面的公式中，折射方向没有严格地按照折射定律计算，而是把出射光向法线靠近得到。

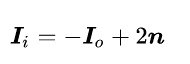
反射方向

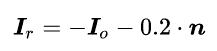
折射方向

计算出射光颜色，不仅要考虑光线追踪得到的颜色，还要考虑折射光线所穿过的液体的颜色。Beer-Lambert定律解释了为什么一杯水是透明的，游泳池泛着蓝光，而大海是深沉的碧蓝。根据Beer–Lambert定律，液体的透光量随液体的厚度呈指数衰减。我们使用修改的Beer-Lambert定律计算折射光的颜色。设液体厚度为T，透光量为A，液体本征颜色I_f。

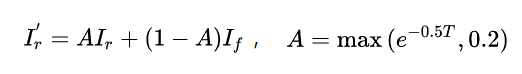
令（上图）其发出射光的颜色是反射颜色和折射颜色的混合，混合的比例由菲涅尔定律给出。菲涅尔定律的计算量较大，计算机图形学中常常使用Schlick公式代替。Schlick公式根据出射光与法线的夹角给出了反射率：

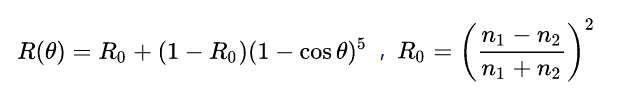
其中n1和n2分别是水和空气的折射率。于是我们终于得出最终的渲染结果。

左：最终渲染
右：反射颜色，折射颜色，厚度染色后折射颜色

可能的改进

还有许多地方能够改进屏幕空间渲染的效果。下面列出几条我能想到的：

• 实现阴影和焦散。焦散的实现可参考： C. Wyman and S. Davis, “Interactive Image-Space
  Techniques for Approximating Caustics,” in Proceedings of the 2006
  Symposium on Interactive 3D Graphics and Games, 2006, pp. 14–17.
• 改进平滑算法。双边滤波算法保留深度的不连续性的同时，也一定程度上保留了粒子边界。
• 借鉴 J. Yu and G. Turk, “Reconstructing surfaces of particle-based
  fluids using anisotropic kernels,” ACM Trans. Graph., vol. 32, no. 1,
  pp. 1–12, Jan. 2013.渲染到深度纹理时，将粒子渲染为椭球形，而不是球形。

脚注

项目地址：https://github.com/naeioi/PBF-CUDA

这是我第一次做管线渲染，也是第一次做物理模拟。项目的选题很大程度上受到了@Raymond Fei的影响。欢迎交流！

---

这是侑虎科技第426篇文章，感谢作者Nae Zhu供稿。欢迎转发分享，未经作者授权请勿转载。如果您有任何独到的见解或者发现也欢迎联系我们，一起探讨。QQ群：793972859（原群已满员）

个人主页：https://www.zhihu.com/people/nae-zhu/activities，作者也是U Sparkle活动参与者，UWA欢迎更多开发朋友加入U Sparkle开发者计划，这个舞台有你更精彩！