微表面模型-PBR渲染管线的材质
- 作者:admin
- /
- 时间:2017年02月24日
- /
- 浏览:12925 次
- /
- 分类:厚积薄发
PBR渲染管线之所以能够比较真实地表现各种不同的材质,是因为它采用了更加复杂的材质模型。在PBR渲染管线出现之前,我们通常采用的材质模型由三部分组成:环境光(Ambient)、漫反射(Diffuse)以及镜面反射(Specular)。我们采用Lambert模型来模拟漫反射散射,用Phong模型来模拟镜面反射高光。但是这种模型难以模拟出表面不同的粗糙程度造成的不同反射效果,导致它模拟出来的材质在视觉上看起来更加接近于塑料的光滑表面。
PBR渲染管线中采用的是一种叫做微表面(Microfacet Model)的材质模型,它基于物理的观察,认为物体表面由很多凹凸不平的微小镜面组成。这些具有不同大小、方向的微表面在对入射光线进行反射时产生了不同的反射效果,从而使得人眼能观察到不同的材质属性。因此,微表面模型能够更加真实地模拟各种不同的材质,如下图所示:

虽然PBR渲染管线是近几年才被应用到游戏渲染领域,但是微表面模型早在上世纪80年代就在计算机图形学领域被提出。今天介绍的这篇技术论文是于1981年发表在ACM Computer Graphics的文章。这篇论文提出了一个对真实世界材质模拟的数学模型,它就是著名的Cook-Torrance模型。Cook-Torrance模型对计算机图形学材质模型的研究发展具有重要的影响。直到今天,我们仍然可以看到许多游戏引擎的PBR渲染管线中采用Cook-Torrance材质模型的简化版以及它的变种。
在这篇论文中的Cook-Torrance模型出现之前,大部分计算机图形学中模拟物体材质模型的设计思路都是基于几何光学,如:模拟理想漫反射的Lambert模型、利用余弦函数指数函数模拟高光的Phong、以及将grazing angle的高光考虑在内的Blinn等。这些模型能够很好地模拟一部分真实世界的材质,但是仍然有些材质无法模拟。Cook-Torrance模型则不同,它基于的是一个物理现象,即物体表面是由许多微小的平面组成。这些平面的朝向各不相同,而对于光滑的物体,微小平面朝向分布比较统一,对于粗糙物体,微小平面的朝向分布更加散乱。这使得Cook-Torrance模型能够更加通用,并且能够模拟表面粗糙的材质。前人提出的模型在模拟镜面反射以及高光的效果时更像是塑料,而Cook-Torrance不仅能模拟塑料,也能很好地模拟金属等粗糙表面的高光现象。
接下来我们将首先介绍文章中的反射光照模型,即Cook-Torrance模型的通用表达式。然后,介绍高光项的表达式。因为基于微表面物理模型与传统的解析模型最大的区别,就在于对镜面反射高光项的处理不同。基于微表面模型的高光项,引入了更多的考虑因素,如:菲涅尔现象、微表面的朝向分布函数、以及阴影遮挡项,才使得其能够成为更加通用材质模型。
一、反射模型
给定光源、物体表面以及观察者,反射模型描述了光线从光源方向射向物体表面,然后从观察者的方向被反射出去的情况。其中,包含了光的强度以及颜色信息。被反射的光的强度和颜色取决于光源射出的光强度和颜色,以及物体表面的反射能力。通常我们用BRDF(Bidirectional Reflectance Distribution Function)函数来描述物体表面对光的反射能力。接下来我们将介绍文章作者是如何定义这个函数的。

物体表面反射能力函数,即 BRDF 函数,可以定义为:从 L 方向射入的光线有多少从 V 方向被射出。假设入射光为无穷远的方向光,并且光强用 Ii 表示,则从 L 方向入射到 P 点的光能可表示为:

其中,ω 为入射光方向角。若用 R 表示 BRDF 函数, Ir 表示反射光线的强度,则 Ir 可表示为:
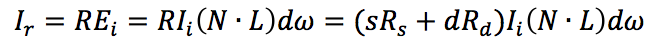
其中,s + d = 1 分别表示高光和漫反射系数。如果再加上环境光影响,则上述公式可变化为:
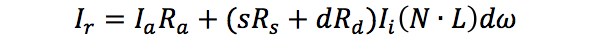
上述公式即为文章中的光照计算表达式。
二、高光项及其中各项表达式
文章作者定义了一个光源方向和视线方向之间的一个向量 H 。如上图所示,给定物体表面一点 P ,以及光源方向 L 和视线方向 V 。则其中间向量可以由如下公式表示:
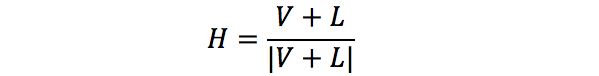
其中,θ 为 L 和 V 之间夹角的一半。因此,
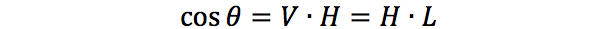
文章作者假设环境光为一个恒定值,漫反射为理想漫反射,于是 Ra 和 Rd 与视线方向无关。但是高光项 Rs 与视线方向有关。根据微表面模型的定义,物体表面由无数朝向不同微小平面组成,每一个微小平面可以看作一个镜面,对入射光产生镜面反射。因此,只有法线方向与 H 相同的微小平面才会对高光项产生贡献。定义高光项的形式为:
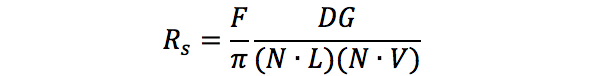
其中,F 为菲涅尔项、G 为阴影遮挡项、D 为朝向分布项。接下来我们将一一介绍这三项的表达式。
首先,我们介绍阴影遮挡项。根据前人提出的模型,G 函数可以用如下公式表示:
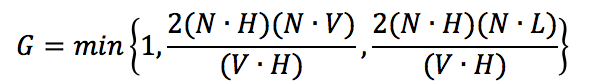
朝向分布函数 D 描述了微小平面中朝向 H 方向的平面的比例。在前人提出的模型中,比较著名的是Blinn和Beckmann提出的模型。Blinn模型的表达式为:
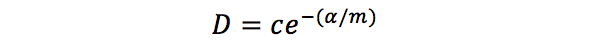
其中,C 为一个常量。Beckmann模型的表达式为:

在这两个模型中,α 表示 H 和 N 之间的夹角,m 则决定了高光的分布范围。m 取值较小时,微小平面的朝向比较统一,因此高光的范围比较窄。反之,则高光的反射范围比较广,如下图所示:

左边两幅图从上到下是当 m = 0.2 和 m = 0.6 时Beckmann模型的反射分布,右边两幅图从上到下是当 m = 0.2 和 m = 0.6 时高斯模型的反射分布。从上图可见,不同的 m 取值代表了不同的表面粗糙度。而当物体表面具有多种不同粗糙度时,分布函数 D 可以用不同取值的 m 的加权平均:
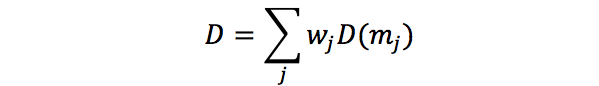
根据前人提出的菲涅尔公式,菲涅尔项 F 可以表示成为:
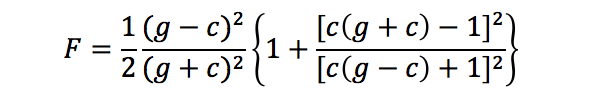
其中,c = cosθ = V·H,g2 =n2 +c2-1。当θ = 0 时,c = 1,g = n。则有:
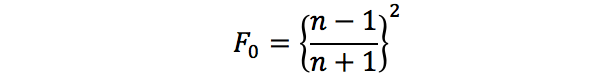
于是,可求得:
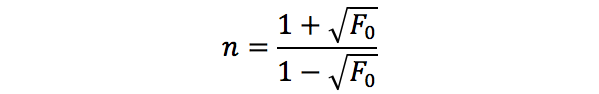
至此,我们介绍完了Cook-Torrance模型中高光项的所有内容。接下来我们将对文章中的渲染结果进行展示。
三、更多结果展示
文章作者用不同的参数渲染了不同材质的物体。如下图所示,不同的模型对应了不同取值的 s ,d 和 m。
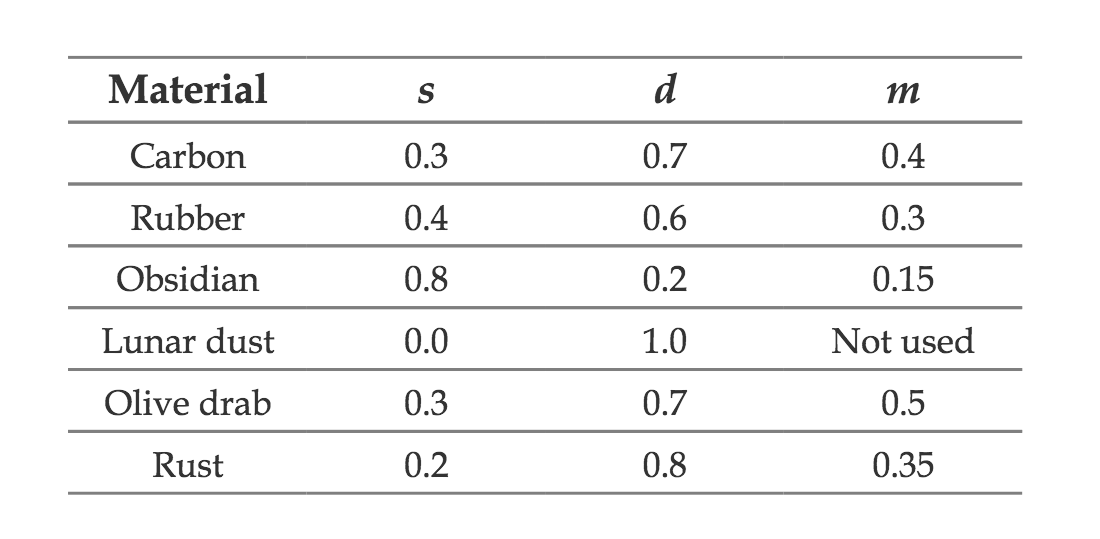
渲染出来的结果如下图所示:

下图是包含多种材质的物体渲染结果:


如上图所示,两幅图都是用Cook-Torrance模型渲染的结果,左边是一个塑料材质的黄色瓶子,右边是一个黄色的铜质瓶子。从上图可以看到,Cook-Torrance模型可以很好地模拟物体表面不同程度粗糙度的光照情况,因此它不仅能渲染出塑料材质表面轮廓清晰的高光,也能渲染出金属表面模糊的高光效果。而这一特性却是传统的模型无法达到的效果。
四、总结
这篇论文基于微表面模型,提出了一个新的材质模型。相比于前人提出的模型,该模型考虑了对菲涅尔现象、阴影遮挡以及微表面朝向分布等因素对高光项的影响。从而使得该模型能够很好地模拟粗糙表面的高光现象。对于不同粗糙度的参数取值,该模型能够更加通用地模拟广泛的材质。
五、论文信息
关于论文作者:
Robert L. Cook,著名计算机图形学学者,毕业于康奈尔大学,是Pixar动画电影公司著名渲染引擎RenderMan的创立者之一,目前已退休。
Kenneth E. Torrance,著名计算机图形学学者,曾经在康奈尔大学机械与航天工程学院工作,目前已退休。
下载地址:
http://inst.cs.berkeley.edu/~cs294-13/fa09/lectures/cookpaper.pdf
这是侑虎科技的原创文章,欢迎转载分享,未经许可请勿转载。
关于惟学无际
UWA在2017年推出的全新研究型专栏,我们将为大家推荐极具实际价值的学术论文,并梳理其中的研究背景、实现原理和执行方法等。内容专注于游戏、VR和AR相关的计算机图形学领域。正所谓问渠哪得清如许,为有源头活水来 ,希望大家在研发的过程中不仅知其然,还能知其所以然。





